Der Merkurtransit 2019: Zugrunde liegende Ideen
| 1. | 2. | 3. | 4. |
 |
 |
 |
 |
Caracas, Venezuela, 14:00:00 UT
(E. Torres) |
Hannover, Deutschland, 14:00:01 UT
(U. Backhaus) |
Caracas
umskaliert und gedreht |
Hannover
beschnitten und gedreht |
Wir veranschaulichen das Vorgehen grafisch anhand zweier Transitfotos aus dem Jahr 2016: Auf den Originalbildern hat die Sonne sowohl unterschiedliche Größen als auch verschiedene Orientierungen (1. und 2.). Deshalb wurde das Foto aus Caracas gedreht und so umskaliert, dass der Sonnenradius auf beiden Bildern gleich groß ist (3.). Im zweiten Schritt wurde auch das Foto aus Hannover gedreht und beschnitten (4.). Um gute quantitative Ergebnisse zu erhalten, müssen diese Schritte rechnerisch durchgeführt werden.
Die Methoden zum Auffinden der Nordrichtung sind etwas kompliziert. Wir beschreiben sie weiter unten.
 |
|---|
Kombination ("max") der geeignet gedrehten und skalierten Bilder von 14:00 UT aus Caracas und Hannover
Merkurs Parallaxe ist wirklich sehr klein. |
Wenn der Winkelradius der Sonne bekannt ist oder gemessen werden kann, dann kann der Parallaxenwinkel
β in dem kombinierten Bild gemessen werden.
zurück zum Seitenanfang
Der Effekt der Parallaxe beschreibt die Tatsache, dass ein astronomisches Objekt vor dem Hintergrund der viel weiter entfernten Fixsterne unterschiedliche Positionen hat, wenn es von verschiedenen Orten auf der Erde aus beobachtet wird. Die Richtungen von den beiden Beobachtern zu dem Objekt unterscheiden sich also. Der Winkel
β zwischen diesen Richtungen ist der sogenannte Parallaxenwinkel (oder einfach die Parallaxe) des Objektes in Bezug auf die beiden Beobachtungsorte. Wenn die Parallaxe eines Objektes bekannt ist, kann daraus seine Entfernung berechnet werden.

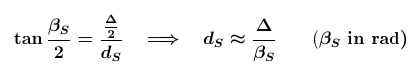
Der Merkurtransit eröffnet die Möglichkeit, die Entfernung zur Sonne zu bestimmen, indem zunächst die Parallaxe von Merkur gemessen wird. Während eines Transits dient die Sonnenscheibe als Bezugssystem für die Positionsmessungen. Dabei entsteht allerdings ein Problem: Auch die Sonne zeigt einen Parallaxeneffekt.
Deshalb ist Merkurs parallaktische Verschiebung gegenüber der Sonne nicht sein Parallaxenwinkel βM.

Zum Glück kann dieses Problem leicht gelöst werden: Da die parallaktische Verschiebung der Sonne dieselbe Richtung hat wie Merkurs, ist die Verschiebung
β, die relativ zur Sonne gemessen wird, einfach die Differenz der beiden Parallaxen:
 | |
 |
Wenn sich der Beobachter von A nach B bewegt,
verschieben sich Merkur und die Sonne um βM und βS in dieselbe Richtung. | |
Wenn die beiden Sonnenbilder übereinander gelegt werden,
wird Merkurs Verschiebung um βS kleiner. |
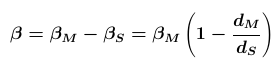
Seit Copernicus und Kepler kann das Verhältnis der Bahnradien der Planeten (oder genauer: das Verhältnis ihrer momentanen Abstände von der Sonne) berechnet werden,
ohne den Wert der Astronomischen Einheit zu kennen. Deshalb kann Merkurs Parallaxenwinkel
βM aus dem gemessenen Winkel
β abgeleitet werden:

zurück zum Seitenanfang
Jetzt können wir auch den Parallaxenwinkel der Sonne berechnen:

oder, noch einfacher:

Wenn wir aber diesen Winkel und die Positionen der beiden Beobachter kennen, können wir auch die Entfernungg zur Sonne ableiten
dS:

Der Winkel
βS - und damit auch der Abstand
dS - hängt vom projizierten linearen Abstand
Δsin w der beiden Beobachter ab. Es ist üblich, den Parallaxenwinkel auf den Radius der Erde
RE zu beziehen. Diesen Winkel nennt man dann die
Parallaxe der Sonne πS oder die
Sonnenparallaxe.

Da die parallakgtische Verschiebung als Bruchteil
f des Winkelradius der Sonne gemessen wird,
β=fρS, erhalten wir nun unsere endgültige Formel zur Bestimmung der Sonnenparallaxe:

und für die Entfernung zwischen Erde und Sonne:

In diesem Projekt werden wir die folgenden Größen als bekannt voraussetzen: 1) den Erdradius, 2) den Winkelradius der Sonne und 3) das Verhältnis der Sonnenabstände von Erde und Merkur. Anders als im
Transitprojekt des Jahres 2004 werden wir die Bestimmung des projizierten Abstandes
Δsin w zwischen den Beobachtern nicht behandeln.
Deshalb werden wir uns auf die sorgfältige Messung der parallaktischen Verschiebung β, bzw. des Verhältnisses f konzentrieren.
zurück zum Seitenanfang
Wir hoffen, unter Punkt 1. dieser Seite deutlich gemacht zu haben, was das zentrale Problem beim Vergleich von verschiedenen Orten aus simultan aufgenommener Fotos ist: die
Bestimmung ihrer Orientierung, also die
Messung der äquatorialen Nordrichtung. Es gibt (mindestens) drei Möglichkeiten zur Lösung dieses Problems:
- Bei gut justierten professionellen Teleskopen auf einer parallaktischen Montierung oder auf einer azimutalen Montierung, die über einen Derotator verfügen, ist häufig keine Bearbeitung erforderlich, weil sie bereits perfekt eingenordet sind.
- Die Ost-West-Richtung zeigt sich in der täglichen Bewegung astronomischer Objekte, die (fast) keine Eigenbewegung besitzen. Man kann sie herausfinden, indem man im Abstand von etwa 2 - 4 Minuten zwei Aufnahmen mit festgehaltener Kamera (abgeschalteter Nachführung) macht und dabei darauf achtet, dass der Mittelpunkt der Sonnenscheibe auf beiden Fotos gut ausgemessen werden kann. Die Verschiebung zwischen den beiden Mittelpunkten zeigt dann die Ost-West-Richtung. Die folgende Bildreihe zeigt das Vorgehen: Zwei Fotos, die im Abstand von 151 s aufgenommen wurden, zeigen die tägliche Bewegung der Sonne in diesem Zeitintervall. Die Bilder können (aber müssen nicht) überlagert werden. Die Bewegungsrichtung kann bestimmt werden, indem die Positionen der beiden Sonnenmittelpunkte gemessen werden. Hier wurde das dadurch getan, dass mit dem kleinen Windows-Programm evaltransitpicts Kreise an den jeweiligen Sonnenrand angepasst wurden. Die Position von Merkur kann dann, z. B. mit demselben Programm, relativ zu der so bestimmten Ost-West-Richtung gemessen werden.
 |
 |
 |
 |
Hannover, 12:00:04
(U. Backhaus) |
Hannover, 12:02:35
(U. Backhaus) |
Hannover, 12::00:04 + 12:02:35
("max"-Kombination) |
Hannover, 12::00:04 + 12:02:35
(Messung der Merkurpositionen) |
-
Falls ein Beobachter die Sonne nur einmal fotografiert hat und die Orientierung nicht erkennbar ist, benötigt man einen deutlich erkennbaren und scharf begrenzten Sonnenfleck auf der Sonne. Dann kann man die Merkurposition relativ zu diesem Sonnenfleck messen (siehe unten) oder das Bild einnorden, z. B. indem man das Bild mit einer zeitgleichen Aufnahme des SDO vergleicht. Wegen des kleineren Abstandes zwischen der Sonnenmitte und dem Sonnenfleck ist diese Methode jedoch deutlich weniger genau als das oben beschriebene Verfahren.
Die folgende Bildreihe veranschaulicht das Verfahren: Zwei gleichzeitig aufgenommene Fotos sind zwar ungefähr, aber nicht genau eingenordet. Um die Merkurpositionen trotzdem vergleichen zu können, werden sie bezüglich der Richtung von der Sonnenmitte zu einem bestimmten Teil des Sonnenflecks bestimmt, die bereits vorher ausgemessen wurde. Dabei wird wieder das Programm evaltransitpicts.
 |
 |
 |
 |
Pointe Saint Mathieu, 17:00:00
(T. Kunzemann) |
Jugendherberge Konstanz, 17:00:00
(Carl Bosch Gymnasium) |
Merkurs Positionswinkel relativ zum Sonnenfleck |
zurück zum Seitenanfang
Zunächst messen wir die Pixelpositionen des Sonnenmittelpunktes
(xS,yS) und Merkurs
(xM,yM) (
x Richtung Westen,
y Richtung Norden). Merkurs Abstand
rM vom Mittelpunkt der Sonne ist dann

Um die Messwerte aus Fotos mit unterschiedlichen Maßstäben vergleichen zu können, drücken wir Abstände als Bruchteile des Winkelradius der Sonne
ρS aus:

Mit den relativen Koordinaten
(xM-xS,y
M-y
S) kann dann Merkurs Positionswinkel
φ0 bezüglich der unteren Bildkante berechnet werden. Kennt man die Orientierung des Bildes, kann dieser Winkel in den korrekten Positionswinkel
φ umgerechnet werden, der von Westen ausgehend entgegen dem Uhrzeigersinn gemessen wird:

Beispiele für dieses Vorgehen werden in unseren
Übungen detailliert beschrieben.
Schließlich ergibt sich Merkurs parallaktische Verschiebung
β zwischen zwei an verschiedenen Orten aufgenommenen Fotos zu
 .
.
Dabei ist
ρS der Winkelradius der Sonne.
Beispiel
Setzt man die korrekte Einnordung der obigen Kombination der 14:00-Bilder aus Caracas und Hannover voraus, dann können die folgenden Merkurpositionen gemessen werden:
x'1=-0.3712, y'1=-0.1891, x'2=-0.3643, y'2=-0.1937 und deshalb β=0.00837ρS.
Mit den bekannten Werten für den Winkelradius der Sonne (15.84') und für die geografischen Positionen der Beobachter findet man (z. B. mit
comp2mercurypositions.xls) einen recht befriedigenden Wert für die Sonnenparallaxe:
πS=8.3"
zurück zum Seitenanfang
 |
 |
Editor: |
Udo Backhaus
 |
last update: 2019-04-03 |
 |







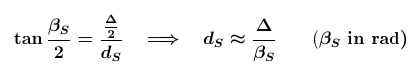

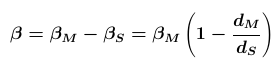
















 .
.